Questo post fa parte di una serie di articoli dedicata agli errori statistici più frequenti che come reviewer, ma anche solo come lettore, mi capita di leggere nella letteratura scientifica.
In questo post #1 della rassegna ti vorrei parlare dell’errore più comune che commettono gli autori nel riportare le statistiche descrittive.
Si tratta dell’uso di media e deviazione standard utilizzate per variabili distribuite in modo non gaussiano.
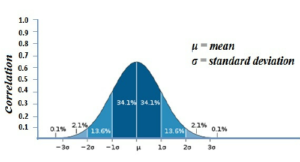
Quando riporti variabili distribuite normalmente, utilizzare media e deviazione standard è corretto e utile perché significa fornire informazioni molto precise: stai dicendo al tuo lettore che circa il 95,5% dei valori della variabile che stai descrivendo rientra nell’intervallo “media ± 2*deviazione standard”, che circa il 99,7% dei valori rientra nell’intervallo “media ±3*deviazione standard”, che il 68,3 rientra nell’intervallo “media ±1*deviazione standard, e così via con tutte le altre caratteristiche della distribuzione normale.
Quando invece descrivi una variabile distribuita in modo non-normale, utilizzare media e deviazione standard non ha più questo tipo di utilità, anzi è addirittura dannoso per il lettore che cerca di interpretare i tuoi dati, perché stai fornendo implicitamente informazioni false.
Devi perciò usare utilizzare altre statistiche descrittive, solitamente mediana (al posto della media) e range interquartile(come dispersione, al posto della distribuzione standard).
Per cui la frase con la quale dovresti cominciare il paragrafo relativo ai metodi statistici, nel più comune dei casi, è qualcosa del tipo:
Categorical data have been summarized in counts and percentages; continuous data have been described by mean and standard deviation when distributed normally. In case of deviation from normality, median and interquartile range were used.